Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders

Abstract

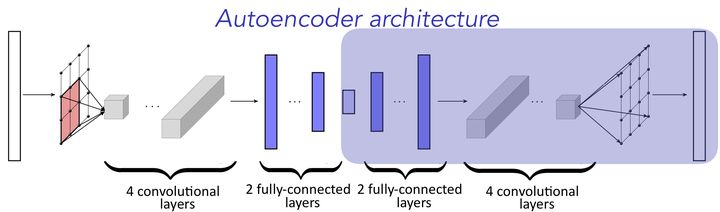
Nearly all model-reduction techniques project the governing equations onto a linear subspace of the original state space. Such subspaces are typically computed using methods such as balanced truncation, rational interpolation, the reduced-basis method, and (balanced) POD. Unfortunately, restricting the state to evolve in a linear trial subspace imposes a fundamental limitation to the accuracy of the resulting reduced-order model (ROM). In particular, linear-subspace ROMs can be expected to produce low-dimensional models with high accuracy only if the problem admits a fast decaying Kolmogorov $n$-width (e.g., diffusion-dominated problems). Unfortunately, many problems of interest exhibit a slowly decaying Komolgorov $n$-width (e.g., advection-dominated problems). To address this, we propose a novel framework for projecting dynamical systems onto nonlinear trial manifolds using minimum-residual formulations at the time-continuous and time-discrete levels; the former leads to manifold Galerkin projection, while the latter leads to manifold least-squares Petrov–Galerkin projection. Next, we show that this manifold can be efficiently computed using convolutional autoencoders from deep learning. Finally, we demonstrate the ability of the method to significantly outperform even the ideal linear-subspace ROM on benchmark advection-dominated problems, thereby demonstrating the method's ability to overcome the intrinsic limitations of linear-subspace ROMs.