An efficient, globally convergent method for optimization under uncertainty using adaptive model reduction and sparse grids
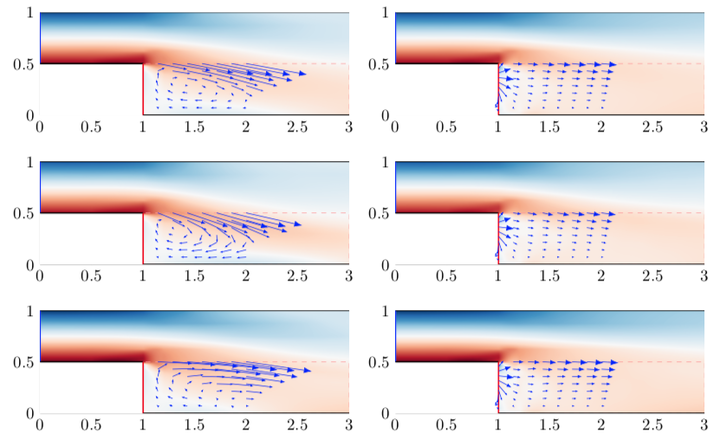 The mean flow (top) and standard deviation offsets (center and bottom) to the uncontrolled (left) and controlled (right) flow.
The mean flow (top) and standard deviation offsets (center and bottom) to the uncontrolled (left) and controlled (right) flow.Abstract
This work introduces a new method to efficiently solve optimization problems constrained by partial differential equations (PDEs) with uncertain coefficients. The method leverages two sources of inexactness that trade accuracy for speed: (1) stochastic collocation based on dimension-adaptive sparse grids (SGs), which approximates the stochastic objective function with a limited number of quadrature nodes, and (2) projection-based reduced-order models (ROMs), which generate efficient approximations to PDE solutions. These two sources of inexactness lead to inexact objective function and gradient evaluations, which are managed by a trust-region method that guarantees global convergence by adaptively refining the sparse grid and reduced-order model until a proposed error indicator drops below a tolerance specified by trust-region convergence theory. A key feature of the proposed method is that the error indicator—which accounts for errors incurred by both the sparse grid and reduced-order model—must be only an asymptotic error bound, i.e., a bound that holds up to an arbitrary constant that need not be computed. This enables the method to be applicable to a wide range of problems, including those where sharp, computable error bounds are not available; this distinguishes the proposed method from previous works. Numerical experiments performed on a model problem from optimal flow control under uncertainty verify global convergence of the method and demonstrate the method's ability to outperform previously proposed alternatives.