Windowed least-squares model reduction for dynamical systems

Abstract

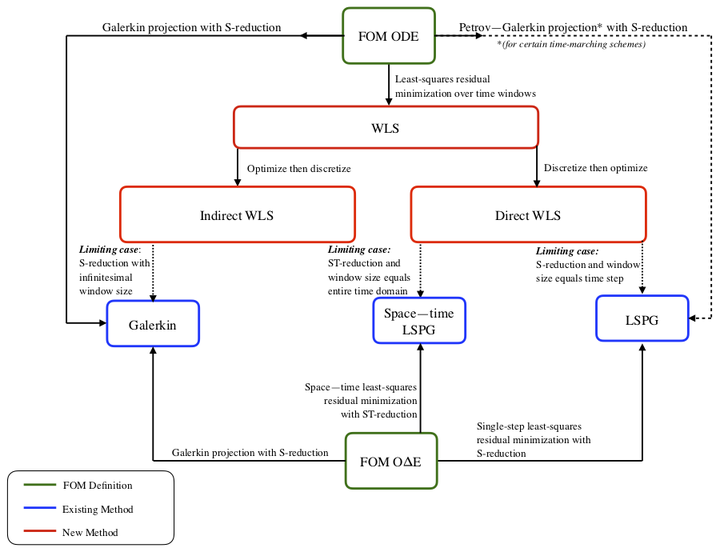
This work proposes a windowed least-squares (WLS) approach for model-reduction of dynamical systems. The proposed approach sequentially minimizes the time-continuous full-order-model residual within a low-dimensional space-time trial subspace over time windows. The approach comprises a generalization of existing model reduction approaches, as particular instances of the methodology recover Galerkin, least-squares Petrov-Galerkin (LSPG), and space-time LSPG projection. In addition, the approach addresses key deficiencies in existing model-reduction techniques, e.g., the dependence of LSPG and space-time LSPG projection on the time discretization and the exponential growth in time exhibited by a posteriori error bounds for both Galerkin and LSPG projection. We consider two types of space-time trial subspaces within the proposed approach: one that reduces only the spatial dimension of the full-order model, and one that reduces both the spatial and temporal dimensions of the full-order model. For each type of trial subspace, we consider two different solution techniques: direct (i.e., discretize then optimize) and indirect (i.e., optimize then discretize). Numerical experiments conducted using trial subspaces characterized by spatial dimension reduction demonstrate that the WLS approach can yield more accurate solutions with lower space-time residuals than Galerkin and LSPG projection.