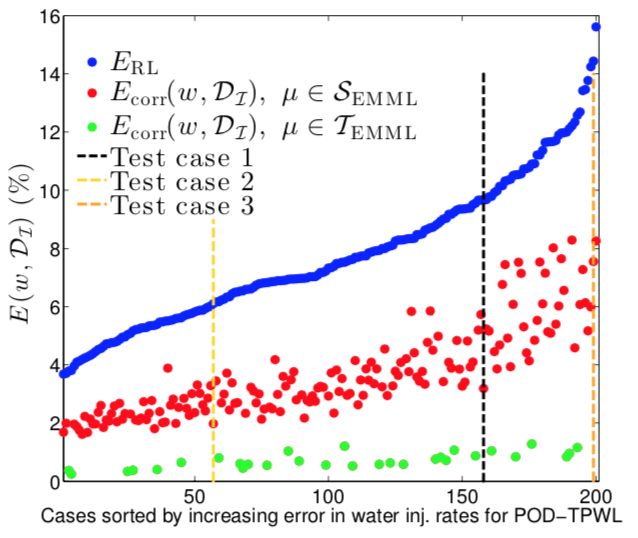
Relative time-integrated error in production and injection rates. Applying the correction provided by the proposed error model method (constructed with random forests) significantly reduces the error in the quantity of interest.Abstract
A machine-learning-based framework for modeling the error introduced by surrogate models of parameterized dynamical systems is proposed. The framework entails the use of high-dimensional regression techniques (e.g., random forests, LASSO) to map a large set of inexpensively computed ‘error indicators’ (i.e., features) produced by the surrogate model at a given time instance to a prediction of the surrogate-model error in a quantity of interest (QoI). This eliminates the need for the user to hand-select a small number of informative features. The methodology requires a training set of parameter instances at which the time-dependent surrogate-model error is computed by simulating both the high-fidelity and surrogate models. Using these training data, the method first determines regression-model locality (via classification or clustering), and subsequently constructs a ‘local’ regression model to predict the time-instantaneous error within each identified region of feature space. We consider two uses for the resulting error model: (1) as a correction to the surrogate-model QoI prediction at each time instance, and (2) as a way to statistically model arbitrary functions of the time-dependent surrogate-model error (e.g., time-integrated errors). We apply the proposed framework to model errors in reduced-order models of nonlinear oil–water subsurface flow simulations, with time-varying well-control (bottom-hole pressure) parameters. The reduced-order models used in this work entail application of trajectory piecewise linearization in conjunction with proper orthogonal decomposition. When the first use of the method is considered, numerical experiments demonstrate consistent improvement in accuracy in the time-instantaneous QoI prediction relative to the original surrogate model, across a large number of test cases. When the second use is considered, results show that the proposed method provides accurate statistical predictions of the time- and well-averaged errors.