Accelerated solution of discrete ordinates approximation to the Boltzmann transport equation via model reduction

Abstract

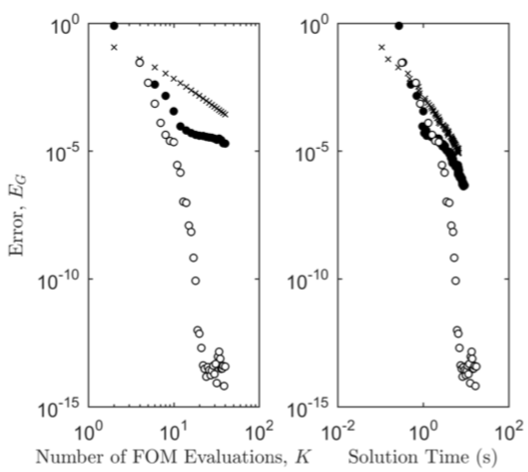
Radiation heat transfer is an important phenomenon in many physical systems of practical interest. When participating media is important, the radiative transfer equation (RTE) must be solved for the radiative intensity as a function of location, time, direction, and wavelength. In many heat-transfer applications, a quasi-steady assumption is valid, thereby removing time dependence. The dependence on wavelength is often treated through a weighted sum of gray gases (WSGG) approach. The discrete ordinates method (DOM) is one of the most common methods for approximating the angular (i.e., directional) dependence. The DOM exactly solves for the radiative intensity for a finite number of discrete ordinate directions and computes approximations to integrals over the angular space using a quadrature rule; the chosen ordinate directions correspond to the nodes of this quadrature rule. This work applies a projection-based model-reduction approach to make high-order quadrature computationally feasible for the DOM for purely absorbing applications. First, the proposed approach constructs a reduced basis from (high-fidelity) solutions of the radiative intensity computed at a relatively small number of ordinate directions. Then, the method computes inexpensive approximations of the radiative intensity at the (remaining) quadra-ture points of a high-order quadrature using a reduced-order model constructed from the reduced basis. This results in a much more accurate solution than might have been achieved using only the ordinate directions used to compute the reduced basis. One-and three-dimensional test problems highlight the efficiency of the proposed method.