Efficient structure-preserving model reduction for nonlinear mechanical systems with application to structural dynamics
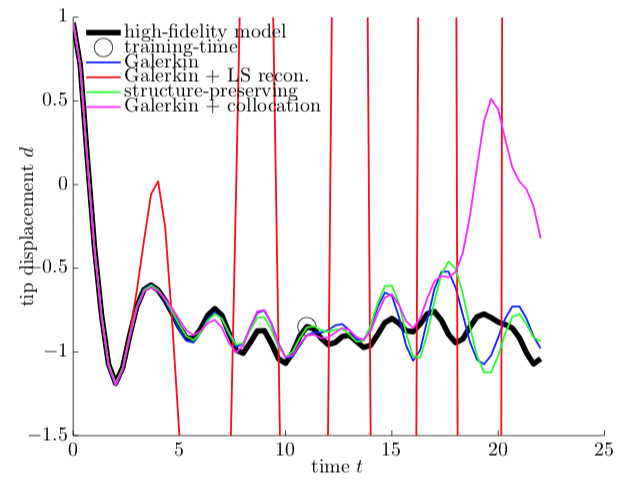Responses generated by all models for a multiple sets of training parameters in a predictive scenario. The proposed structure-preserving method is the only method equipped with model reduction that generates an accurate response.Abstract
This work proposes a model-reduction methodology that both preserves Lagrangian structure and leads to computationally inexpensive models, even in the presence of high-order nonlinearities. We focus on parameterized simple mechanical systems under Rayleigh damping and external forces, as structural-dynamics models often fit this description. The proposed model-reduction methodology directly approximates the quantities that define the problem’s Lagrangian structure: the Riemannian metric, the potential-energy function, the dissipation function, and the external force. These approxi- mations preserve salient properties (e.g., positive definiteness), behave similarly to the functions they approximate, and ensure computational efficiency. Results applied to a simple parameterized truss- structure problem demonstrate the importance of preserving Lagrangian structure and illustrate the method’s ability to generate speedups while maintaining observed stability, in contrast with other model-reduction techniques that do not preserve structure.