Preserving Lagrangian structure in nonlinear model reduction with application to structural dynamics
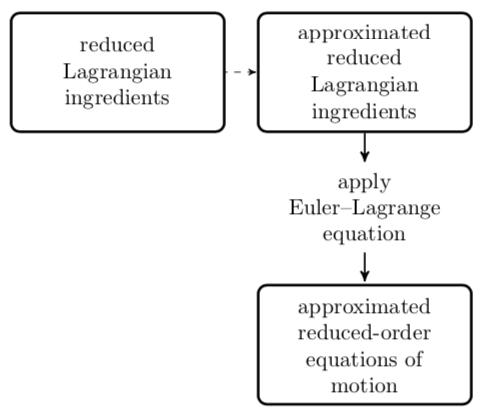 By approximating Lagrangian ingredients before deriving the equations of motion, the approach preserves Lagrangian structure.
By approximating Lagrangian ingredients before deriving the equations of motion, the approach preserves Lagrangian structure.Abstract
This work proposes a model-reduction methodology that preserves Lagrangian structure and achieves computational efficiency in the presence of high-order nonlinearities and arbitrary parameter dependence. As such, the resulting reduced-order model retains key properties such as energy conservation and symplectic time-evolution maps. We focus on parameterized simple mechanical systems subjected to Rayleigh damping and external forces, and consider an application to nonlinear structural dynamics. To preserve structure, the method first approximates the system's ‘Lagrangian ingredients’—the Riemannian metric, the potential-energy function, the dissipation function, and the external force—and subsequently derives reduced-order equations of motion by applying the (forced) Euler–Lagrange equation with these quantities. From the algebraic perspective, key contributions include two efficient techniques for approximating parameterized reduced matrices while preserving symmetry and positive definiteness: matrix gappy proper orthogonal decomposition and reduced-basis sparsification. Results for a parameterized truss-structure problem demonstrate the practical importance of preserving Lagrangian structure and illustrate the proposed method's merits: it reduces computation time while maintaining high accuracy and stability, in contrast to existing nonlinear model-reduction techniques that do not preserve structure.