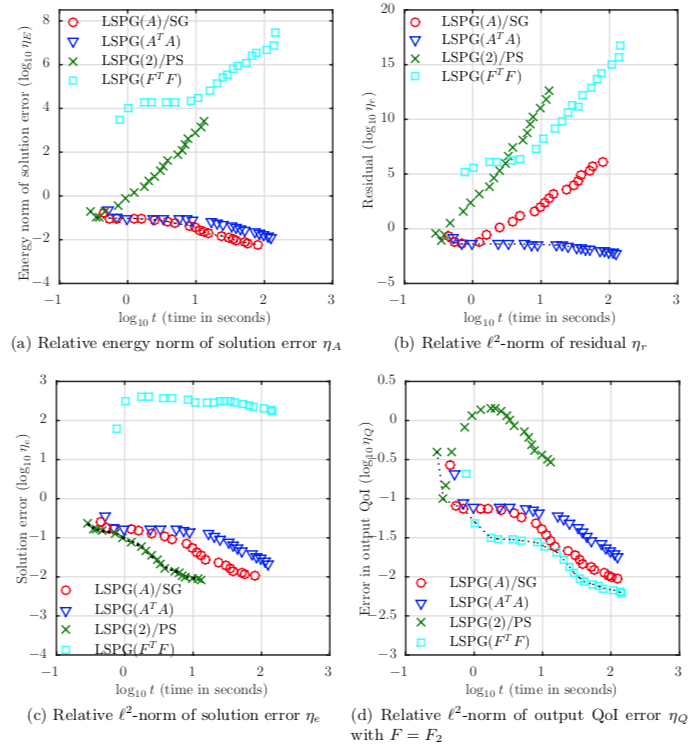
Pareto front of relative error measures versus wall time for varying polynomial degree $p$ ($p$ varies from 1 to 20 in increments of 1 going from left to right) for diffusion problem 3: gamma random coefficient and random forcing. Note that each method is Pareto optimal in terms of minimizing its targeted error measure and computational wall time.Abstract
We consider the numerical solution of parameterized linear systems where the system matrix, the solution, and the right-hand side are parameterized by a set of uncertain input parameters. We explore spectral methods in which the solutions are approximated in a chosen finite-dimensional subspace. It has been shown that the stochastic Galerkin projection technique fails to minimize any measure of the solution error [A. Mugler and H.-J. Starkloff, ESAIM Math. Model. Numer. Anal., 47 (2013), pp. 1237–1263]. As a remedy for this, we propose a novel stochatic least-squares Petrov– Galerkin (LSPG) method. The proposed method is optimal in the sense that it produces the solution that minimizes a weighted l2-norm of the residual over all solutions in a given finite-dimensional subspace. Moreover, the method can be adapted to minimize the solution error in different weighted $l^2$-norms by simply applying a weighting function within the least-squares formulation. In addition, a goal-oriented seminorm induced by an output quantity of interest can be minimized by defining a weighting function as a linear functional of the solution. We establish optimality and error bounds for the proposed method, and extensive numerical experiments show that the weighted LSPG method outperforms other spectral methods in minimizing corresponding target weighted norms.