Recovering missing CFD data for high-order discretizations using deep neural networks and dynamics learning
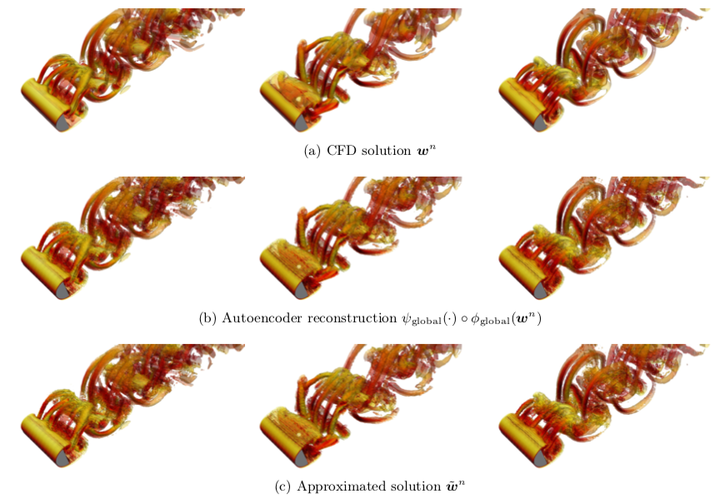 Instantaneous iso-surfaces of Q-criterion colored by velocity magnitude at $n =1000$, $4 000$, and $7 000$.
Instantaneous iso-surfaces of Q-criterion colored by velocity magnitude at $n =1000$, $4 000$, and $7 000$.Abstract
Data I/O poses a significant bottleneck in large-scale CFD simulations; thus, practitioners would like to significantly reduce the number of times the solution is saved to disk, yet retain the ability to recover any field quantity (at any time instance) a posteriori. The objective of this work is therefore to accurately recover missing CFD data a posteriori at any time instance, given that the solution has been written to disk at only a relatively small number of time instances. We consider in particular high-order discretizations (e.g., discontinuous Galerkin), as such techniques are becoming increasingly popular for the simulation of highly separated flows. To satisfy this objective, this work proposes a methodology consisting of two stages: 1) dimensionality reduction and 2) dynamics learning. For dimensionality reduction, we propose a novel hierarchical approach. First, the method reduces the number of degrees of freedom within each element of the high-order discretization by applying autoencoders from deep learning. Second, the methodology applies principal component analysis to compress the global vector of encodings. This leads to a low-dimensional state, which associates with a nonlinear embedding of the original CFD data. For dynamics learning, we propose to apply regression techniques (e.g., kernel methods) to learn the discrete-time velocity characterizing the time evolution of this low-dimensional state. A numerical example on a large-scale CFD example characterized by nearly 13 million degrees of freedom illustrates the suitability of the proposed method in an industrial setting.