Space–time least-squares Petrov–Galerkin projection for nonlinear model reduction

Abstract

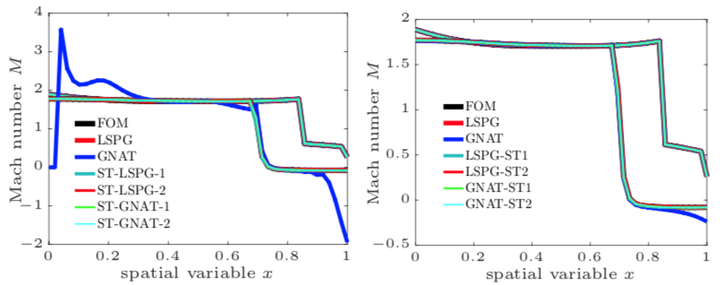
This work proposes a space–time least-squares Petrov–Galerkin (ST-LSPG) projection method for model reduction of nonlinear dynamical systems. In contrast to typical nonlinear model-reduction methods that first apply (Petrov–)Galerkin projection in the spatial dimension and subsequently apply time integration to numerically resolve the resulting low-dimensional dynamical system, the proposed method applies projection in space and time simultaneously. To accomplish this, the method first introduces a low-dimensional space–time trial subspace, which can be obtained by computing tensor decompositions of state-snapshot data. The method then computes discrete-optimal approximations in this space–time trial subspace by minimizing the residual arising after time discretization over all space and time in a weighted $l^2$-norm. This norm can be defined to enable complexity reduction (i.e., hyper-reduction) in time, which leads to space–time collocation and space–time GNAT variants of the ST-LSPG method. Advantages of the approach relative to typical spatial-projection-based nonlinear model reduction methods such as Galerkin projection and least-squares Petrov–Galerkin projection include: (1) a reduction of both the spatial and temporal dimensions of the dynamical system, (2) the possibility of removing of spurious temporal modes (e.g., unstable growth) from the state space, and (3) error bounds that exhibit slower growth in time. Numerical examples performed on model problems in fluid dynamics demonstrate the ability of the method to generate orders-of-magnitude computational savings relative to spatial-projection-based reduced-order models without sacrificing accuracy for a fixed spatio-temporal discretization.