An adaptive POD-Krylov reduced-order model for structural optimization
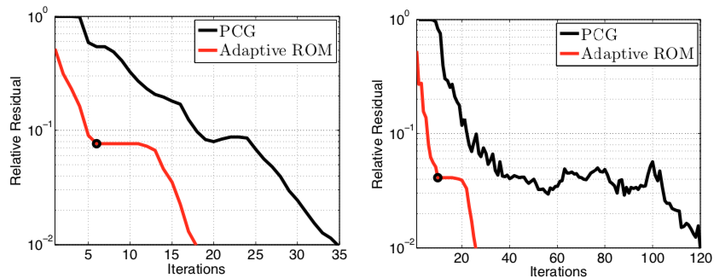 Convergence of the relative residual for the first RHS at two online parameter instances.
Convergence of the relative residual for the first RHS at two online parameter instances.Abstract
We present an adaptive proper orthogonal decomposition (POD)-Krylov reduced-order model (ROM) for structural optimization. At each step of the optimization loop, we compute approximate solutions to the structural state and sensitivity equations using a novel POD-augmented conjugate gradient (CG) algorithm. This algorithm consists of three stages. In the first two stages, the solution component in the POD subspace is computed using a CG algorithm. Here, fast convergence is ensured due to well- conditioned reduced equations. This property results from using an energy inner product to compute the POD basis. In the third stage, the solution is refined in an adaptively-computed Krylov subspace using an augmented preconditioned CG algorithm. The dimension of the Krylov subspace is increased until the prescribed tolerance is satisfied. This methodology can be considered a reduced-order modeling technique, as it efficiently computes approximate states and sensitivities in the sum of two subspaces. The ROM is well-suited for optimization settings because its accuracy is continually improved as the optimum is approached. We report on the benchmarking of the proposed method for a direct sensitivity analysis of a parameterized V-22 tiltrotor wing panel. The results highlight the ability of the proposed method to compute approximate solutions to the structural state and sensitivity equations at a significantly lower cost than the typical augmented preconditioned CG method.