Time-series machine-learning error models for approximate solutions to parameterized dynamical systems
LSTM regression with residual-based features outperform other methods within the T-MLEM frameworkAbstract
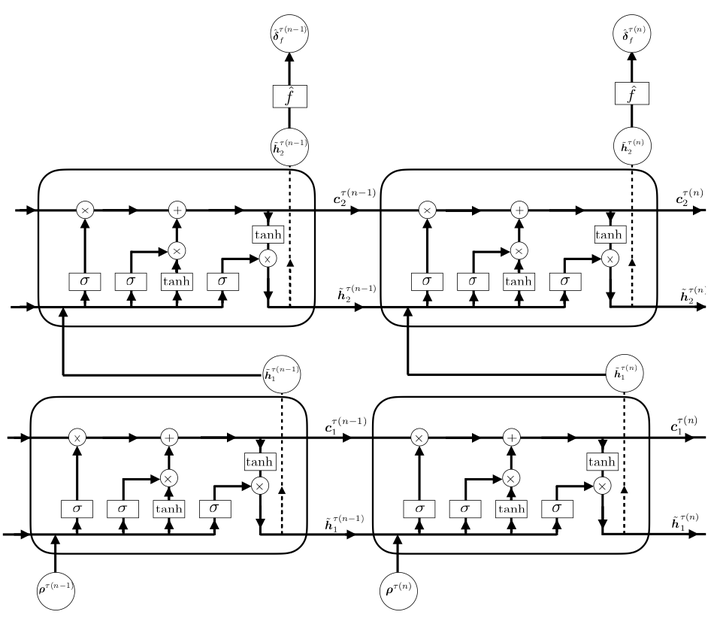
This work proposes a machine-learning framework for modeling the error incurred by approximate solutions to parameterized dynamical systems. In particular, we extend the machine-learning error models (MLEM) framework proposed in [Freno, Carlberg, 2019] to dynamical systems. The proposed Time-Series Machine-Learning Error Modeling (T-MLEM) method constructs a regression model that maps features—which comprise error indicators that are derived from standard a posteriori error-quantification techniques—to a random variable for the approximate-solution error at each time instance. The proposed framework considers a wide range of candidate features, regression methods, and additive noise models. We consider primarily recursive regression techniques developed for time-series modeling, including both classical time-series models (e.g., autoregressive models) and recurrent neural networks (RNNs), but also analyze standard non-recursive regression techniques (e.g., feed-forward neural networks) for comparative purposes. Numerical experiments conducted on multiple benchmark problems illustrate that the long short-term memory (LSTM) neural network, which is a type of RNN, outperforms other methods and yields substantial improvements in error predictions over traditional approaches.