The network uncertainty quantification method for propagating uncertainties in component-based systems
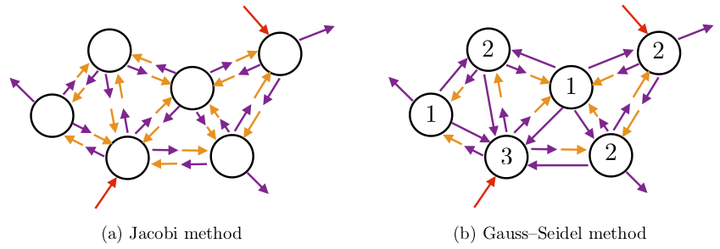Relaxation methods. Here, random variables that were computed at the previous iteration are shown in orange, random variables that are computed at the current iteration are shown in violet, and exogenous-input random variables—whose values are fixed—are shown in red.Abstract
This work introduces the network uncertainty quantification (NetUQ) method for performing uncertainty propagation in systems composed of interconnected components. The method assumes the existence of a collection of components, each of which is characterized by exogenous-input random variables (e.g., material properties), endogenous-input random variables (e.g., boundary conditions defined by another component), output random variables (e.g., quantities of interest), and a local uncertainty-propagation operator (e.g., provided by stochastic collocation) that computes output random variables from input random variables. The method assembles the full-system network by connecting components, which is achieved simply by associating endogenous-input random variables for each component with output random variables from other components; no other inter-component compatibility conditions are required. The network uncertainty-propagation problem is: Compute output random variables for all components given all exogenous-input random variables. To solve this problem, the method applies classical relaxation methods (i.e., Jacobi and Gauss–Seidel iteration with Anderson acceleration), which require only blackbox evaluations of component uncertainty-propagation operators. Compared with other available methods, this approach is applicable to any network topology (e.g., no restriction to feed-forward or two-component networks), promotes component independence by enabling components to employ tailored uncertaintypropagation operators, supports general functional representations of random variables, and requires no offline preprocessing stage. Also, because the method propagates functional representations of random variables throughout the network (and not, e.g., probability density functions), the joint distribution of any set of random variables throughout the network can be estimated a posteriori in a straightforward manner. We perform supporting convergence and error analysis and execute numerical experiments that demonstrate the weak- and strong-scaling performance of the method.