A method for interpolating on manifolds structural dynamics reduced-order models
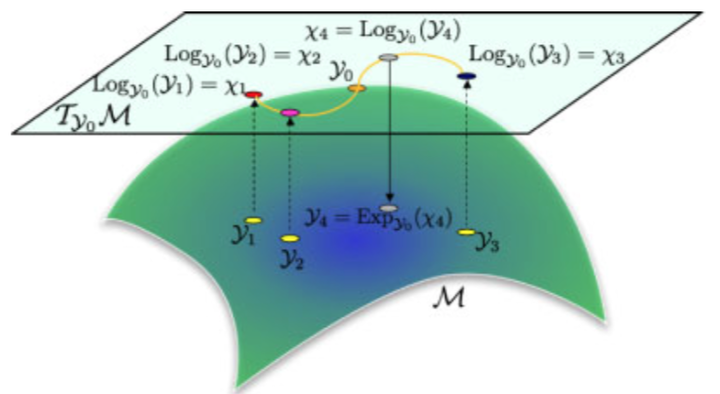Graphical description of the generalized interpolation of the matrices $ Y_i$ in a tangent space to a matrix manifold $M$.Abstract
A rigorous method for interpolating a set of parameterized linear structural dynamics reduced‐order models (ROMs) is presented. By design, this method does not operate on the underlying set of parameterized full‐order models. Hence, it is amenable to an online real‐time implementation. It is based on mapping appropriately the ROM data onto a tangent space to the manifold of symmetric positive‐definite matrices, interpolating the mapped data in this space and mapping back the result to the aforementioned manifold. Algorithms for computing the forward and backward mappings are offered for the case where the ROMs are derived from a general Galerkin projection method and the case where they are constructed from modal reduction. The proposed interpolation method is illustrated with applications ranging from the fast dynamic characterization of a parameterized structural model to the fast evaluation of its response to a given input. In all cases, good accuracy is demonstrated at real‐time processing speeds.