Efficient non-linear model reduction via a least-squares Petrov–Galerkin projection and compressive tensor approximations
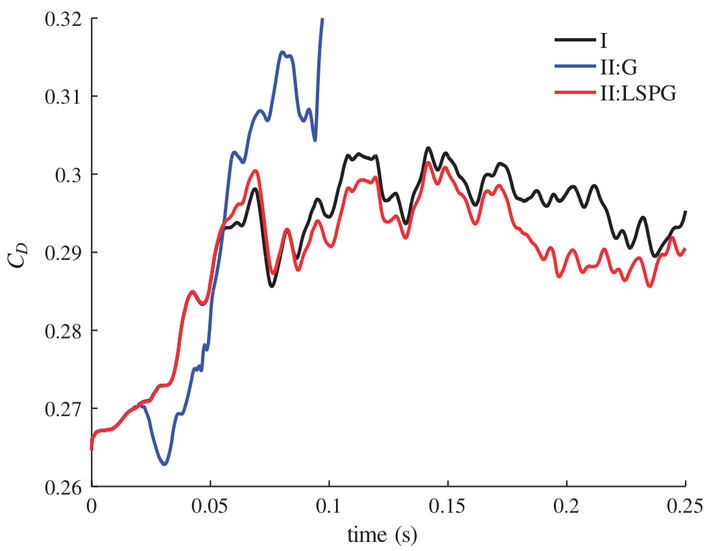 First results reported demonstrating the superior predictive performance of least-squares Petrov–Galerkin projection relative to Galerkin projection. Results obtained on the Ahmed-body geometry.
First results reported demonstrating the superior predictive performance of least-squares Petrov–Galerkin projection relative to Galerkin projection. Results obtained on the Ahmed-body geometry.Abstract
A Petrov–Galerkin projection method is proposed for reducing the dimension of a discrete non‐linear static or dynamic computational model in view of enabling its processing in real time. The right reduced‐order basis is chosen to be invariant and is constructed using the Proper Orthogonal Decomposition method. The left reduced‐order basis is selected to minimize the two‐norm of the residual arising at each Newton iteration. Thus, this basis is iteration‐dependent, enables capturing of non‐linearities, and leads to the globally convergent Gauss–Newton method. To avoid the significant computational cost of assembling the reduced‐order operators, the residual and action of the Jacobian on the right reduced‐order basis are each approximated by the product of an invariant, large‐scale matrix, and an iteration‐dependent, smaller one. The invariant matrix is computed using a data compression procedure that meets proposed consistency requirements. The iteration‐dependent matrix is computed to enable the least‐squares reconstruction of some entries of the approximated quantities. The results obtained for the solution of a turbulent flow problem and several non‐linear structural dynamics problems highlight the merit of the proposed consistency requirements. They also demonstrate the potential of this method to significantly reduce the computational cost associated with high‐dimensional non‐linear models while retaining their accuracy