Structure-preserving model reduction for marginally stable LTI systems
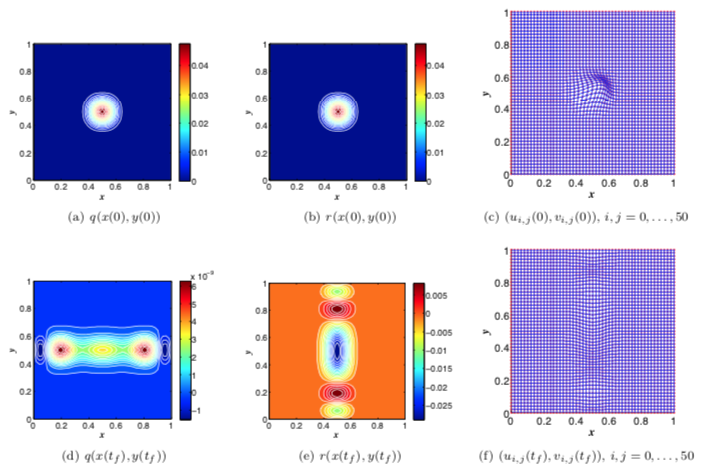 2D mass–spring example. Initial condition and final state, where the proposed method incurs neglible errors.
2D mass–spring example. Initial condition and final state, where the proposed method incurs neglible errors.Abstract
This work proposes a structure-preserving model reduction method for marginally stable linear time-invariant (LTI) systems. In contrast to Lyapunov-stability-based approaches—which ensure the poles of the reduced system remain in the open left-half plane—the proposed method preserves marginal stability by reducing the subsystem with poles on the imaginary axis in a manner that ensures those poles remain purely imaginary. In particular, the proposed method decomposes a marginally stable LTI system into (1) an asymptotically stable subsystem with eigenvalues in the open left-half plane and (2) a pure marginally stable subsystem with a purely imaginary spectrum. We propose a method based on inner-product projection and the Lyapunov inequality to reduce the first subsystem while preserving asymptotic stability. In addition, we demonstrate that the pure marginally stable subsystem is a generalized Hamiltonian system; we then propose a method based on symplectic projection to reduce this subsystem while preserving pure marginal stability. In addition, we propose both inner-product and symplectic balancing methods that balance the operators associated with two quadratic energy functionals while preserving asymptotic and pure marginal stability, respectively. We formulate a geometric perspective that enables a unified comparison of the proposed inner-product and symplectic projection methods. Numerical examples illustrate the ability of the method to reduce the dimensionality of marginally stable LTI systems while retaining accuracy and preserving marginal stability; further, the resulting reduced-order model yields a finite infinite-time energy, which arises from the pure marginally stable subsystem.