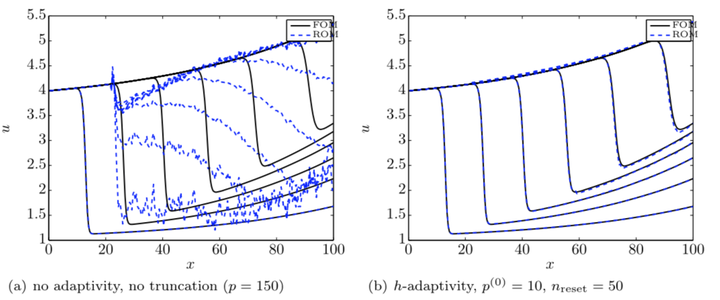
 Comparison of solutions computed by proper orthogonal decomposition–Galerkin with and without $h$-adaptivity.
Comparison of solutions computed by proper orthogonal decomposition–Galerkin with and without $h$-adaptivity.Abstract
This work presents a method to adaptively refine reduced‐order models a posteriori without requiring additional full‐order‐model solves. The technique is analogous to mesh‐adaptive $h$‐refinement: it enriches the reduced‐basis space online by ‘splitting’ a given basis vector into several vectors with disjoint support. The splitting scheme is defined by a tree structure constructed offline via recursive $k$‐means clustering of the state variables using snapshot data. The method identifies the vectors to split online using a dual‐weighted‐residual approach that aims to reduce error in an output quantity of interest. The resulting method generates a hierarchy of subspaces online without requiring large‐scale operations or full‐order‐model solves. Further, it enables the reduced‐order model to satisfy any prescribed error tolerance regardless of its original fidelity, as a completely refined reduced‐order model is mathematically equivalent to the original full‐order model. Experiments on a parameterized inviscid Burgers equation highlight the ability of the method to capture phenomena (e.g., moving shocks) not contained in the span of the original reduced basis.