The GNAT method for nonlinear model reduction: Effective implementation and application to computational fluid dynamics and turbulent flows
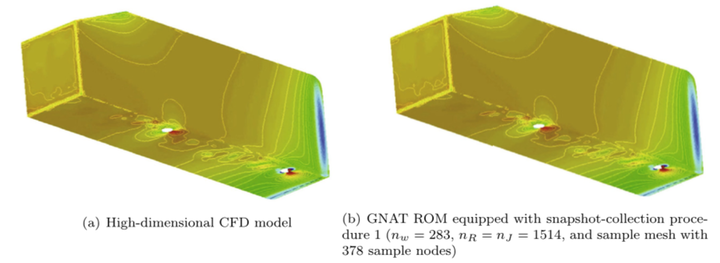 Surface-pressure contours at $t= 0.1 ext{s}$.
Surface-pressure contours at $t= 0.1 ext{s}$.Abstract
The Gauss–Newton with approximated tensors (GNAT) method is a nonlinear model-reduction method that operates on fully discretized computational models. It achieves dimension reduction by a Petrov–Galerkin projection associated with residual minimization; it delivers computational efficiency by a hyper-reduction procedure based on the ‘gappy POD’ technique. Originally presented in Ref. [1], where it was applied to implicit nonlinear structural-dynamics models, this method is further developed here and applied to the solution of a benchmark turbulent viscous flow problem. To begin, this paper develops global state-space error bounds that justify the method’s design and highlight its advantages in terms of minimizing components of these error bounds. Next, the paper introduces a ‘sample mesh’ concept that enables a distributed, computationally efficient implementation of the GNAT method in finite-volume-based computational-fluid-dynamics (CFD) codes. The suitability of GNAT for parameterized problems is highlighted with the solution of an academic problem featuring moving discontinuities. Finally, the capability of this method to reduce by orders of magnitude the core-hours required for large-scale CFD computations, while preserving accuracy, is demonstrated with the simulation of turbulent flow over the Ahmed body. For an instance of this benchmark problem with over 17 million degrees of freedom, GNAT outperforms several other nonlinear model-reduction methods, reduces the required computational resources by more than two orders of magnitude, and delivers a solution that differs by less than 1% from its high-dimensional counterpart.