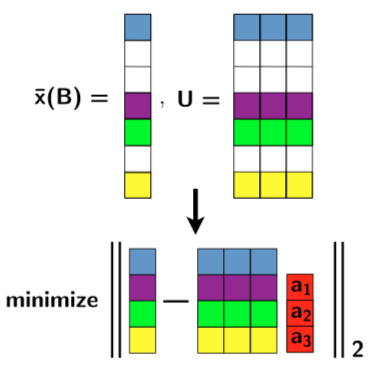
 Least-squares reconstruction example.
Least-squares reconstruction example.Abstract
This paper applies the Gappy proper orthogonal decomposition method, a recently-developed quantitative methodology for reconstructing unknown data, to archaeological problems and highlights the benefits of the method for quantitative analysis within the field. There are three main advantages of the method over polynomial regression, which is most commonly used for missing data problems. First of all, the method can be applied to problems where there are more attributes (variables) than complete samples (samples without missing data). Secondly, the method generates principal components (i.e. eigensamples) as a byproduct of its prediction algorithm; these principal components are useful for characterizing data sets and quantitatively assessing their dominant trends. Thirdly, the method employs fewer ad hoc modelling choices compared with standard regression, as it uses empirically-derived basis functions (the principal components) to make predictions. The Gappy proper orthogonal decomposition method is applied to two case studies on Roman housing focusing on the sites of Pompeii and Herculaneum. These case studies highlight the merits of the method and provide a new quantitative assessment of housing characteristics of the area, a subject which has been primarily analyzed impressionistically. The study concludes by offering extensions and future directions for applying the methodology.