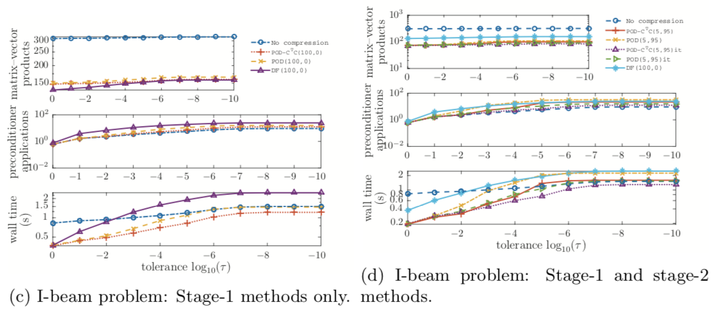
Output-oriented truncation experiments: Average number of matrix-vector products, preconditioner applications, and wall time to compute solutions as a function of the output-oriented tolerance τ. Note that (average) preconditioner applications below 1 indicate that the solution sat- isfied the specified tolerance before entering stage 3Abstract
This work presents a new Krylov-subspace-recycling method for efficiently solving sequences of linear systems of equations characterized by varying right-hand sides and symmetric-positive-definite matrices. As opposed to typical truncation strategies used in recycling such as deflation, we propose a truncation method inspired by goal-oriented proper orthogonal decomposition (POD) from model reduction. This idea is based on the observation that model reduction aims to compute a low-dimensional subspace that contains an accurate solution; as such, we expect the proposed method to generate a low-dimensional subspace that is well suited for computing solutions that can satisfy inexact tolerances. In particular, we propose specific goal-oriented POD ‘ingredients’ that align the optimality properties of POD with the objective of Krylov-subspace recycling. To compute solutions in the resulting ‘augmented’ POD subspace, we propose a hybrid direct/iterative three-stage method that leverages (1) the optimal ordering of POD basis vectors, and (2) well-conditioned reduced matrices. Numerical experiments performed on solid-mechanics problems highlight the benefits of the proposed method over existing approaches for Krylov-subspace recycling.