Decreasing the temporal complexity for nonlinear, implicit reduced-order models by forecasting
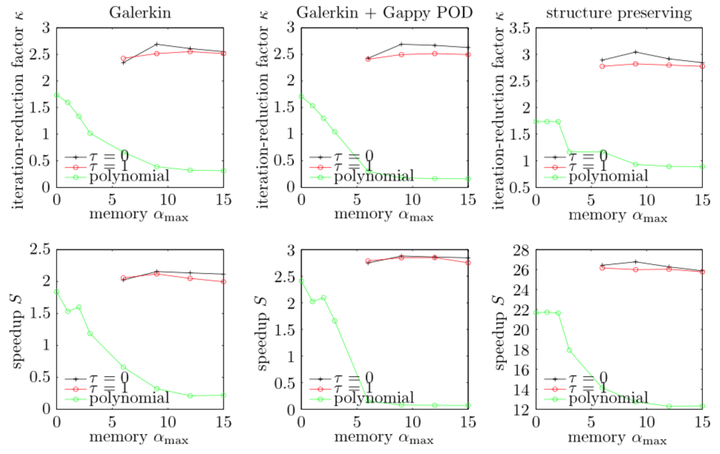The proposed forecasting method decreases both the number of required Newton iterations and simulation time compared with polynomial extrapolation in nearly all cases.Abstract
Implicit numerical integration of nonlinear ODEs requires solving a system of nonlinear algebraic equations at each time step. Each of these systems is often solved by a Newton-like method, which incurs a sequence of linear-system solves. Most model-reduction techniques for nonlinear ODEs exploit knowledge of a system’s spatial behavior to reduce the computational complexity of each linear-system solve. However, the number of linear-system solves for the reduced-order simulation often remains roughly the same as that for the full-order simulation. We propose exploiting knowledge of the model’s temporal behavior to (1) forecast the unknown variable of the reduced-order system of nonlinear equations at future time steps, and (2) use this forecast as an initial guess for the Newton-like solver during the reduced-order-model simulation. To compute the forecast, we propose using the Gappy POD technique. The goal is to generate an accurate initial guess so that the Newton solver requires many fewer iterations to converge, thereby decreasing the number of linear-system solves in the reduced-order-model simulation.