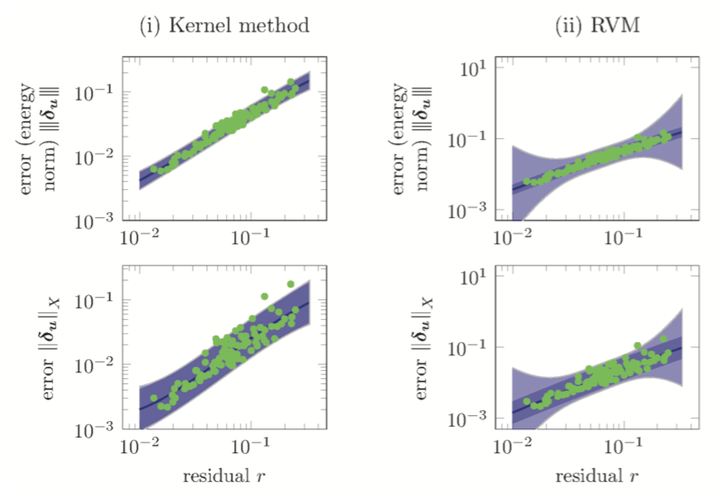
Visualization of ROMES surrogates, computed using the (i) Gaussian-process kernel method and (ii) relevance vector machine.Abstract
This work presents a technique for statistically modeling errors introduced by reduced-order models. The method employs Gaussian-process regression to construct a mapping from a small number of computationally inexpensive ‘error indicators’ to a distribution over the true error. The variance of this distribution can be interpreted as the (epistemic) uncertainty introduced by the reduced-order model. To model normed errors, the method employs existing rigorous error bounds and residual norms as indicators; numerical experiments show that the method leads to a near-optimal expected effectivity in contrast to typical error bounds. To model errors in general outputs, the method uses dual-weighted residuals—which are amenable to uncertainty control—as indicators. Experiments illustrate that correcting the reduced-order-model output with this surrogate can improve prediction accuracy by an order of magnitude; this contrasts with existing ‘multifidelity correction’ approaches, which often fail for reduced-order models and suffer from the curse of dimensionality. The proposed error surrogates also lead to a notion of ‘probabilistic rigor’; i.e., the surrogate bounds the error with specified probability.