Deep Conservation: A latent dynamics model for exact satisfaction of physical conservation laws
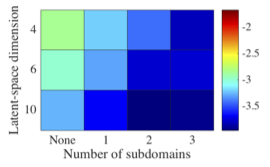 Global state errors of Deep LSPG (None) and Deep conservation (at least one subdomain over which conservation is enforced)
Global state errors of Deep LSPG (None) and Deep conservation (at least one subdomain over which conservation is enforced)Abstract
This work proposes an approach for latent dynamics learning that exactly enforces physical conservation laws. The method comprises two steps. First, we compute a low-dimensional embedding of the high-dimensional dynamical-system state using deep convolutional autoencoders. This defines a low-dimensional nonlinear manifold on which the state is subsequently enforced to evolve. Second, we define a latent dynamics model that associates with a constrained optimization problem. Specifically, the objective function is defined as the sum of squares of conservation-law violations over control volumes in a finite-volume discretization of the problem; nonlinear equality constraints explicitly enforce conservation over prescribed subdomains of the problem. The resulting dynamics model-which can be considered as a projection-based reduced-order model-ensures that the time-evolution of the latent state exactly satisfies conservation laws over the prescribed subdomains. In contrast to existing methods for latent dynamics learning, this is the only method that both employs a nonlinear embedding and computes dynamics for the latent state that guarantee the satisfaction of prescribed physical properties. Numerical experiments on a benchmark advection problem illustrate the method's ability to significantly reduce the dimensionality while enforcing physical conservation.