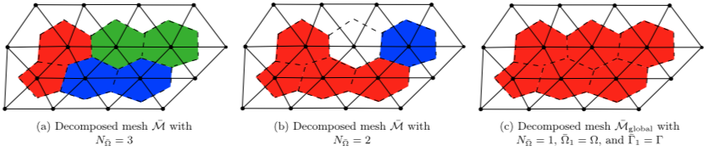
Examples of decomposed meshes for a vertex-centered finite-volume model. Solid lines denote the primal mesh, and dashed lines the control-volume interfaces defining the dual mesh, and colors denote separate subdomains.Abstract
This work proposes a method for model reduction of finite-volume models that guarantees the resulting reduced-order model is conservative, thereby preserving the structure intrinsic to finite-volume discretizations. The proposed reduced-order models associate with optimization problems characterized by a minimum-residual objective function and nonlinear equality constraints that explicitly enforce conservation over subdomains. Conservative Galerkin projection arises from formulating this optimization problem at the time-continuous level, while conservative least-squares Petrov–Galerkin (LSPG) projection associates with a time-discrete formulation. We equip these approaches with hyper-reduction techniques in the case of nonlinear flux and source terms, and also provide approaches for handling infeasibility. In addition, we perform analyses that include deriving conditions under which conservative Galerkin and conservative LSPG are equivalent, as well as deriving a posteriori error bounds. Numerical experiments performed on a parameterized quasi-1D Euler equation demonstrate the ability of the proposed method to ensure not only global conservation, but also significantly lower state-space errors than nonconservative reduced-order models such as standard Galerkin and LSPG projection