A low-cost, goal-oriented ‘compact proper orthogonal decomposition’ basis for model reduction of static systems
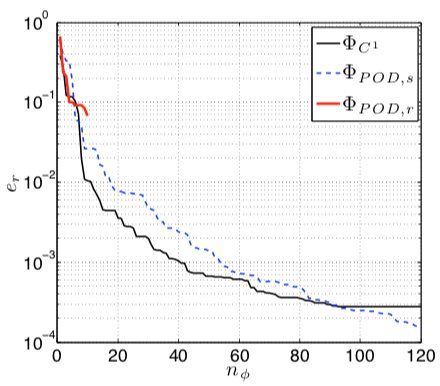 Dependence of relative error on basis dimension for proposed method (black), traditional POD with the same number of parameter samples (red), and traditional POD with the same number of total snapshots—and thus many more parameter samples (dashed blue).
Dependence of relative error on basis dimension for proposed method (black), traditional POD with the same number of parameter samples (red), and traditional POD with the same number of total snapshots—and thus many more parameter samples (dashed blue).Abstract
Reduced basis methods are powerful tools that can significantly speed up computationally expensive analyses in a variety of ‘many-query’ and real-time applications, including de- sign optimization. Unfortunately, these techniques produce reduced-order models (ROMs) that are costly to construct and are not always robust in the parameter space. Further- more, efforts to apply these methods to optimization have almost exclusively relied on offline sampling procedures, which can exacerbate these problems and even prevent com- putational cost savings from being realized. Although adaptive sampling techniques have been recently developed to avoid these drawbacks, their application has been limited to the optimization of dynamical systems. We therefore present a Compact POD (CPOD) basis that treats the (possibly high-order) state vector sensitivities as system ‘snapshots’ and employs a snapshot-weighting scheme to compute a reduced basis. Since sensitivities directly represent the effect of parameter changes on the system’s physics and can often be efficiently computed, the proposed method produces an inherently robust, inexpensive ROM that is well-suited for optimization. We also show that it can be used to extend adaptive sampling procedures to static systems. To test the validity of the CPOD basis, we compare it with the typical POD approach on the analysis of a plane elasticity prob- lem parameterized by shape and material property variables. We find that the proposed methodology leads to solutions of similar (often better) accuracy, at a lower cost, and using many fewer reference configurations than the typical procedure.