A low-cost, goal-oriented ‘compact proper orthogonal decomposition’ basis for model reduction of static systems
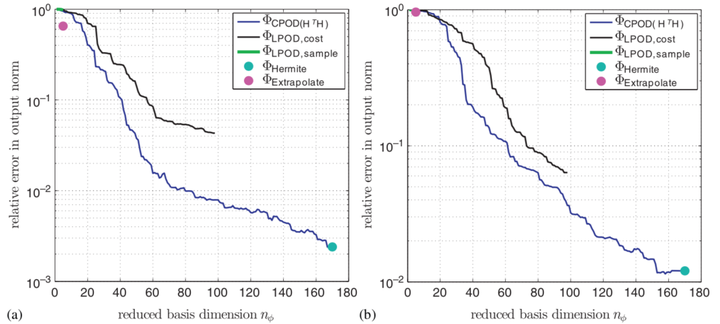 Relative error in the output-induced norm for two online points. The proposed compact POD method yields substantially lower errors for fixed reduced-basis dimension.
Relative error in the output-induced norm for two online points. The proposed compact POD method yields substantially lower errors for fixed reduced-basis dimension.Abstract
A novel model reduction technique for static systems is presented. The method is developed using a goal‐oriented framework, and it extends the concept of snapshots for proper orthogonal decomposition (POD) to include (sensitivity) derivatives of the state with respect to system input parameters. The resulting reduced‐order model generates accurate approximations due to its goal‐oriented construction and the explicit ‘training’ of the model for parameter changes. The model is less computationally expensive to construct than typical POD approaches, since efficient multiple right‐hand side solvers can be used to compute the sensitivity derivatives. The effectiveness of the method is demonstrated on a parameterized aerospace structure problem.
Type
Publication
International Journal for Numerical Methods in Engineering, Vol. 86, No. 3, p. 381–402 (2011)