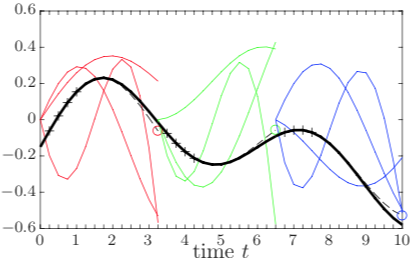
Local forecast with 3 coarse time intervals. Here, the time evolution basis vectors are denoted by thin colored lines, the state entry is denoted by a thick black line, the sampled state is denoted by $+$ markers, and the forecast is denoted by circular markers.Abstract
This work proposes a data-driven method for enabling the efficient, stable time-parallel numerical solution of systems of ordinary differential equations (ODEs). The method assumes that low-dimensional bases that accurately capture the time evolution of the state are available. The method adopts the parareal framework for time parallelism, which is defined by an initialization method, a coarse propagator, and a fine propagator. Rather than employing usual approaches for initialization and coarse propagation, we propose novel data-driven techniques that leverage the available time-evolution bases. The coarse propagator is defined by a forecast (proposed in Ref. [12]) applied locally within each coarse time interval, which comprises the following steps: (1) apply the fine propagator for a small number of time steps, (2) approximate the state over the entire coarse time interval using gappy POD with the local time-evolution bases, and (3) select the approximation at the end of the time interval as the propagated state. We also propose both local-forecast and global-forecast initialization. The method is particularly well suited for POD-based reduced-order models (ROMs). In this case, spatial parallelism quickly saturates, as the ROM dynamical system is low dimensional; thus, time parallelism is needed to enable lower wall times. Further, the time-evolution bases can be extracted from the (readily available) right singular vectors arising during POD computation. In addition to performing analyses related to the method's accuracy, speedup, stability, and convergence, we also numerically demonstrate the method's performance. Here, numerical experiments on ROMs for a nonlinear convection-reaction problem demonstrate the method's ability to realize near-ideal speedups; global-forecast initialization with a local-forecast coarse propagator leads to the best performance.